Гравитационные силы. закон всемирного тяготения

Формула закона всемирного тяготения с объяснениями

Зная массы двух тел и расстояние между ними, можно рассчитать силу их взаимного притяжения с помощью такой формулы:

\
\(F \left( \text{Н} \right)\) (Ньютоны) — сила, с которой два шарообразных тела притягиваются
\( m_{1} \left( \mbox{кг} \right) \) (килограммы) — масса первого тела
\( m_{2} \left( \text{кг} \right) \) (килограммы) — масса второго тела
\( R \left( \text{м} \right) \) (метры) — расстояние между центрами тел
\(G \ = 6{,}67 \cdot 10^{-11} \left( \text{Н} \cdot \frac{\text{м}^2}{\text{кг}^2} \right)\) — гравитационная постоянная

Примечания:

• формула позволяет точно рассчитать притяжение между двумя однородными шарами;
• если тела не шарообразные, или не однородные, то силу притяжения получим с погрешностью;
• чем больше расстояние между телами, тем меньше будет погрешность;

Словесная формулировка закона всемирного тяготения

Закон всемирного тяготения словами можно сформулировать так:

Два тела притягиваются с силойпрямо пропорциональноймассам этих тели обратно пропорциональнойквадрату расстояния между телами.

Пояснения к закону всемирного тяготения

Сила прямо пропорциональна массам тел. Математики прямую пропорциональность записывают так:
\

Прямая пропорциональность означает: чем больше массы, тем больше сила притяжения.

Сила обратно пропорциональна расстоянию в квадрате. Математики обратную пропорциональность записывают с помощью дроби. В знаменателе этой дроби находится величина, обратно пропорциональная величине, находящейся в левой части выражения:
\
Обратная пропорциональность означает: чем больше расстояние между телами, тем меньше сила притяжения.

Аномалии и неточности

Есть некоторые наблюдения, которые не учитываются должным образом, что может указывать на необходимость в более совершенных теориях гравитации или, возможно, быть объясненными другими способами.

Кривая вращения типичной спиральной галактики: предсказанная ( А ) и наблюдаемая ( Б ). Расхождение кривых связано с темной материей .

• Сверхбыстрые звезды : Звезды в галактиках следуют распределению скоростей, когда звезды на окраинах движутся быстрее, чем они должны, в соответствии с наблюдаемым распределением нормальной материи. Галактики в скоплениях галактик демонстрируют похожую картину. Темная материя , которая взаимодействует посредством гравитации, но не электромагнитно, может объяснить это несоответствие. Также были предложены различные модификации ньютоновской динамики .
• Аномалия пролета : различные космические аппараты испытывали большее ускорение, чем ожидалось, во времяманевров по гравитации .
• Ускорение расширения : кажется, что метрическое расширение пространства ускоряется. Для объяснения этого была предложена темная энергия . Недавнее альтернативное объяснение состоит в том, что геометрия пространства неоднородна (из-за скоплений галактик) и что, когда данные интерпретируются заново, чтобы учесть это, расширение в конце концов не ускоряется, однако этот вывод оспаривается.
• Аномальное увеличение астрономической единицы : недавние измерения показывают, что быстрее, чем если бы это происходило исключительно за счет потери массы Солнцем за счет излучения энергии.
• Фотоны с дополнительной энергией : фотоны, проходящие через скопления галактик, должны набирать энергию, а затем снова терять ее на выходе. Ускоряющееся расширение Вселенной должно остановить фотоны, возвращающие всю энергию, но даже с учетом этого фотоны космического микроволнового фонового излучения получают в два раза больше энергии, чем ожидалось. Это может указывать на то, что гравитация спадает быстрее, чем в обратном квадрате на определенных масштабах расстояний.
• Сверхмассивные водородные облака : спектральные линии леса Лайман-альфа предполагают, что водородные облака более сгруппированы в определенных масштабах, чем ожидалось, и, как темный поток , может указывать на то, что гравитация спадает медленнее, чем обратный квадрат на определенных масштабах расстояний.

Гравитационные поля

Гравитационное поле Земли

Гравитационное поле – это расстояние, в пределах которого осуществляется гравитационное взаимодействие между объектами во Вселенной. Чем больше масса объекта, тем сильнее его гравитационное поле – тем ощутимее его воздействие на другие физические тела в пределах определенного пространства. Гравитационное поле объекта потенциально. Суть предыдущего утверждения заключается в том, что если ввести потенциальную энергию притяжения между двумя телами, то она не изменится после перемещения последних по замкнутому контуру. Отсюда выплывает еще один знаменитый закон сохранения суммы потенциальной и кинетической энергии в замкнутом контуре.

В материальном мире гравитационное поле имеет огромное значения. Им обладают все материальные объекты во Вселенной, у которых есть масса. Гравитационное поле способно влиять не только на материю, но и на энергию. Именно за счет влияния гравитационных полей таких крупных космических объектов, как черные дыры, квазары и сверхмассивные звезды, образуются солнечные системы, галактики и другие астрономические скопления, которым свойственна логическая структура.

Последние научные данные показывают, что знаменитый эффект расширения Вселенной так же основан на законах гравитационного взаимодействия. В частности расширению Вселенной способствуют мощные гравитационные поля, как небольших, так и самых крупных ее объектов.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации, называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух точечных или сферических тел в пустом пространстве. Эта задача в рамках классической механики решается аналитически в замкнутой форме; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе эта неустойчивость не позволяет предсказать точно движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: Солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — сложная структура колец Сатурна.

Несмотря на попытки точно описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

В каких случаях справедлив закон всемирного тяготения

Выявленная Ньютоном зависимость имеет ограничения в области применения. Так, закон справедлив только в случаях, когда:

1. тела можно принять материальными точками, то есть их размеры настолько малы по отношению к расстоянию, что ими можно пренебречь;
2. тела обладают сферической формой, что свидетельствует об однородном распределении массы внутри них;
3. одно из тел – шар большого диаметра, а второе имеет несопоставимо маленькие размеры.

когда справедлив закон всемирного тяготения

Соотношение неприменимо, если требуется описать взаимодействие шара и стержня бесконечной длины. В этом случае сила притяжения будет пропорциональна не квадрату расстоянию, а его модулю. А если существует потребность определить тяготение между бесконечной плоскостью и телом, расстояние вообще не будет иметь влияния.

Границы применимости

Несмотря на то, что закон всемирного тяготения Ньютона объясняет работу множества явлений, в конце XIX века было выявлено несоответствие наблюдаемого и рассчитанного смещения перигелия Меркурия. Эта особенность движения планеты не объяснялась известным законом, что потребовало новое понимание гравитации.

Кроме того, на рубеже веков применимость классической механики, основанной на законах Ньютона, подверглась ограничениям. Получение точных результатов с её помощью возможно только в случаях, когда:

• скорость тел гораздо меньше скорости звука;
• размеры объектов гораздо больше размеров атомов и молекул;
• скорость распространения гравитации считается бесконечной.

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Учимся летать

В серии книг Дугласа Адамса «‎Автостопом по Галактике»‎ говорится, что летать — это просто промахиваться мимо Земли. Если ты промахнулся мимо Земли и достиг первой космической скорости 7,9 км/с, то ты стал искусственным спутником Земли.

Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него так получалось, аппарат должен иметь начальную скорость, равную или большую первой космической скорости.

Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.

Подробнее о возможностях полетов и невесомости читайте в нашей статье про вес тела.

Альтернативные теории

Исторические альтернативные теории

• Аристотелевская теория гравитации
• Теория гравитации Ле Сажа (1784) также называлась гравитацией Лесажа, но первоначально была предложена Фатио и развита Жоржем-Луи Ле Сажем на основе объяснения на основе жидкости, в котором легкий газ заполняет всю Вселенную.
• Теория гравитации Ритца , Ann. Chem. Phys. 13, 145, (1908) pp. 267–271, Электродинамика Вебера-Гаусса в применении к гравитации. Классическое продвижение перигелии.
• Теория гравитации Нордстрема (1912, 1913), один из первых конкурентов общей теории относительности.
• Теория Калуцы Клейна (1921)
• Теория гравитации Уайтхеда (1922), еще один ранний конкурент общей теории относительности.

Современные альтернативные теории

• Теория гравитации Бранса – Дике (1961)
• Индуцированная гравитация (1967), предложение Андрея Сахарова, согласно которому общая теория относительности могла возникнуть из квантовых полевых теорий материи.
• Теория струн (конец 1960-х)
• ƒ (R) гравитация (1970)
• Теория Хорндески (1974)
• Супергравитация (1976)
• В модифицированной ньютоновской динамике (MOND) (1981) Мордехай Милгром предлагает модификацию второго закона движения Ньютона для малых ускорений.
• Самосоздание космология теория гравитации (1982) Г. А. Барбер , в которых теория Отруби-Дике модифицирован , чтобы создать массовый
• Петлевая квантовая гравитация (1988) Карло Ровелли , Ли Смолина и Абхая Аштекара
• Несимметричная гравитационная теория (NGT) (1994) Джона Моффата
• Тензорно-векторно-скалярная гравитация (TeVeS) (2004), релятивистская модификация MOND Якоба Бекенштейна.
• Теория хамелеона (2004) Джастина Хури и Аманды Велтман .
• Теория давления (2013) Оливье Минаццоли и Орелиен Хис .
• Конформная гравитация
• Гравитация как энтропийная сила , гравитация, возникающая как явление, возникающее из термодинамической концепции энтропии.
• В теории сверхтекучего вакуума гравитация и искривленное пространство-время возникают как коллективная мода возбуждения нерелятивистской фоновой сверхтекучей жидкости .
• Массивная гравитация , теория, в которой гравитоны и гравитационные волны имеют ненулевую массу

Гравитационные силы: определение

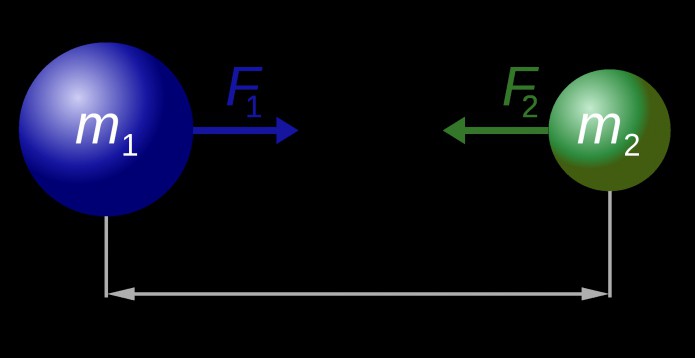
Первая количественная теория гравитации, основанная на наблюдениях движения планет, была сформулирована Исааком Ньютоном в 1687 году в его знаменитых «Началах натуральной философии». Он писал, что силы притяжения, которые действуют на Солнце и планеты, зависят от количества вещества, которое они содержат. Они распространяются на большие расстояния и всегда уменьшаются как величины, обратные квадрату расстояния. Как же можно вычислить эти гравитационные силы? Формула для силы F между двумя объектами с массами m₁ и m₂, находящимися на расстоянии r, такова:

F=Gm1m2/r2,где G — константа пропорциональности, гравитационная постоянная.

Что такое всемирное тяготение

Земля — это большой магнит, который притягивает к себе всё, что находится рядом: и карандаш, случайно выскользнувший из пальцев рук, и астероид, пролетающий мимо. С начала развития науки учёные давали своё видение и определение явлению всемирного тяготения, но только в 1687 году в фундаментальной работе Исаака Ньютона «Математические начала натуральной философии» было доказано его существование и воздействие на окружающие объекты.

математические начала натуральной философии

Интересный факт. Одно из первых изданий книги «Principia Mathematica» было продано на аукционных торгах за 3,7 миллиона долларов.

Основываясь на известные к тому времени эмпирические соотношения Иоганна Кеплера, описывающие гелиоцентрическую картину мира, Ньютон определил закон, согласно которому все тела притягиваются друг к другу.

гелиоцентрическая система мира

Причём сила взаимодействия растёт с увеличением массы и в то же время связана с расстоянием между объектами обратной квадратичной зависимостью, т.е.:

F = G∙(m₁∙m₂/ r2)

Несмотря на то, что объектами относительно небольшой массы данное явление практически не воспринимается, именно гравитация управляет движением астрономических тел, а формулировка закона позволяет объяснить, почему планеты движутся вокруг Солнца, а Луна – вокруг Земли.

Есть ли в космосе гравитация

Когда мы смотрим кино о космосе или видим трансляцию с МКС, в которой космонавты парят в невесомости, многие из нас думают, что там нет гравитации. Это ошибка.

На самом деле гравитация на орбите не то, что есть, она там почти ничем не отличается от той, что мы ощущаем на Земле. Если брать расстояние от центра Земли до МКС, то оно будет примерно на 10 процентов больше расстояния от центра Земли до ее поверхности. Если вспомнить, что гравитация зависит от размера тел и от их расстояния друг от друга, то становится понятно, что гравитация на орбите сильно меньше земной.

Космонавты могут ощущать невесомость не из-за того, что на орбите нет гравитации, а из-за того, что они постоянно находятся в состоянии свободного падения вместе со своим кораблем или космической станцией. Тем не менее, если поставить огромную стремянку и подняться на верхнюю ступеньку, которая будет на высоте орбиты МКС, мы не взлетим, а будем стоять на ней. Сила нашего притяжения немного изменится, но не настолько, чтобы взлететь.

Это не из-за отсутствия гравитации, а наоборот, из-за того, что она есть.

Если говорить совсем просто, космическая станция на орбите движется с огромной скоростью и постоянно стремится как бы пролететь мимо Земли. Ее гравитация в свою очередь удерживает станцию от ”улета”. В итоге, космонавты с их кораблем крутятся вокруг Земли и за счет центробежной силы находятся в уравновешенном состоянии невесомости. Получается, что гравитация на орбите есть и более того, именно она позволяет космонавтам испытывать невесомость, как бы парадоксально это не прозвучало.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Сила тяготения между двумя телами уменьшится в 2 раза, если массу каждого тела

1) увеличить в √2 раз
2) уменьшить в √2 раз
3) увеличить в 2 раза
4) уменьшить в 2 раза

2. Массу каждого из двух однородных шаров увеличили в 4 раза. Расстояние между ними тоже увеличили в 4 раза. Сила тяготения между ними

1) увеличилась в 64 раза
2) увеличилась в 16 раз
3) увеличилась в 4 раза
4) не изменилась

3. В вершинах прямоугольника расположены тела одинаковой массы. Со стороны какого тела на тело 1 действует наибольшая сила?

1) со стороны тела 2
2) со стороны тела 3
3) со стороны тела 4
4) со стороны всех тел одинаковая

4. Закон всемирного тяготения справедлив

A. Для всех тел
Б. Для однородных шаров
B. Для материальных точек

Правильный ответ

1) А
2) только Б
3) только В
4) и А, и Б

5. На ящик массой 5 кг, лежащий на полу лифта, движущегося с ускорением ​\( a \)​ вертикально вниз, действует сила тяжести

1) равная 50 Н
2) большая 50 Н
3) меньшая 50 Н
4) равная 5 Н

6. Сравните значения силы тяжести ​\( F_э \)​, действующей на груз на экваторе, с силой тяжести \( F_м \), действующей на этот же груз на широте Москвы, если груз находится на одной и той же высоте относительно поверхности Земли.

1) ​\( F_э=F_м \)​
2) \( F_э>F_м \)​
3) \( F_э<F_м \)​
4) ответ может быть любым в зависимости от массы тел

7. Сила тяжести, действующая на космонавта на поверхности Луны,

1) больше силы тяжести, действующей на него на поверхности Земли
2) меньше силы тяжести, действующей на него на поверхности Земли
3) равна силе тяжести, действующей на него на поверхности Земли
4) больше силы тяжести, действующей на него на поверхности Земли на экваторе, и меньше силы тяжести, действующей на него, на поверхности Земли на полюсе

8. Сила тяжести, действующая на тело, зависит от

А. Географической широты местности
Б. Скорости падения тела на поверхность Земли

Правильный ответ

1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б

9. Какое(-ие) из утверждений верно(-ы)?

Сила тяжести, действующая на тело у поверхности некоторой планеты, зависит от

А. Массы планеты.
Б. Массы тела.

1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б

10. Первая космическая скорость зависит

A. От радиуса планеты
Б. От массы планеты
B. От массы спутника

Правильный ответ

1) только А
2) только Б
3) только А и Б
4) А, Б, В

11. Установите соответствие между физической величиной (левый столбец) и формулой, выражающей её взаимосвязь с другими величинами (правый столбец). В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Сила тяжести
Б. Ускорение свободного падения на поверхности Земли
B. Закон всемирного тяготения

ФОРМУЛА
1) ​\( F=G\frac{m_1m_2}{r^2} \)​
2) ​\( F_т=mg \)​
3) ​\( g=G\frac{M_З}{(R_З+h)^2} \)​
4) ​\( g=G\frac{M_З}{R^2} \)​

12. Среди приведённых утверждений выберите два правильных и запишите их номера в таблицу

1) Гравитационная постоянная показывает, с какой силой притягиваются друг к другу два тела массой 1 кг.
2) Значение силы тяжести, действующей на тело, зависит от скорости его движения.
3) Ускорение свободного падения зависит от массы и радиуса планеты.
4) При увеличении расстояния между телами в 3 раза сила тяготения между ними уменьшается в 9 раз.
5) Изменение массы одного из взаимодействующих тел не влияет на значение силы тяготения.

Часть 2

13. Человек на Земле притягивается к ней с силой 700 Н. С какой силой он притягивался бы к Марсу, находясь на его поверхности, если радиус Марса в 2 раза меньше радиуса Земли, а масса в 10 раз меньше, чем масса Земли?

Квантовая гравитация

Универсальной квантовой теории, объяснившей бы само понятие гравитации, ещё не разработано. Для представления гравитационного взаимодействия было бы вероятно предложить гравитонный обмен, в котором гравитоны выступают в качестве калибровочных бозонов со спином 2. Но такая теория не считается удовлетворительной. На существующее время есть несколько подходов, разрешающих квантование гравитации. Эти подходы считаются достаточно перспективными.

• Теория струн. Она заменяет частицы фона пространства-времени на струны и браны (подобие струн). Для решения многомерных задач, браны видятся как частицы уже многомерные, но в тоже время они и структуры пространства-времени. Гравитоны здесь становятся состоянием струн, а не отдельными частицами. Хотя низкие энергии их к ним и причисляют.
• Петлевая квантовая гравитация. Здесь время и пространство являются дискретными частями. Они не привязаны к фону пространства-времени, являясь квантовыми пространственными ячейками. Они между собой соединены таким образом, что в малых временных масштабах представляются дискретной структурой пространства. При укрупнении масштабов, части плавно становятся непрерывным пространством-временем. Петлевая гравитация способна описать сущность Большого взрыва, а также пролить свет на его преддверие. Это даже позволяет обходиться без привлечения бозона Хиггса.

Ускорение

Казалось бы, если требуется достичь g, равного земному, нужно всего лишь придать кораблю плоскую (платформообразную) форму, и заставить его двигаться по перпендикуляру к плоскости с нужным ускорением. Таким путем будет получена искусственная гравитация, причем – идеальная.

Однако в реальности все гораздо сложнее.

В первую очередь стоит учесть топливный вопрос. Для того чтобы станция постоянно ускорялась, необходимо иметь бесперебойный источник питания. Даже если внезапно появится двигатель, не выбрасывающий материю, закон сохранения энергии останется в силе.

Вторая проблема заключается в самой идее постоянного ускорения. Согласно нашим знаниям и физическим законам, невозможно ускоряться до бесконечности.

Кроме того, такой транспорт не подходит для исследовательских миссий, поскольку он должен постоянно ускоряться – лететь. Он не сможет остановиться для изучения планеты, он даже медленно пролететь вокруг нее не сможет – надо ускоряться.

Таким образом, становится ясно, что и такая искусственная гравитация нам пока недоступна.

Отношение к универсальному закону

Закон всемирного тяготения Ньютона утверждает, что между любыми двумя массами существует гравитационная сила, равная по величине для каждой массы и выровненная так, чтобы притягивать две массы друг к другу. Формула:

Fзнак равнограммм1м2р2 {\ Displaystyle F = G {\ гидроразрыва {m_ {1} m_ {2}} {r ^ {2}}} \}

где и — любые две массы, — гравитационная постоянная и — расстояние между двумя точечными массами.
м1{\ displaystyle m_ {1}}м2{\ displaystyle m_ {2}}грамм{\ displaystyle G}р{\ displaystyle r}

Два тела вращаются вокруг своего центра масс (красный крест)

Используя интегральную форму закона Гаусса , эту формулу можно распространить на любую пару объектов, один из которых намного массивнее другого — например, планета относительно любого артефакта человеческого масштаба. Расстояния между планетами и между планетами и Солнцем (на много порядков) больше, чем размеры Солнца и планет. Вследствие этого и Солнце, и планеты можно рассматривать как точечные массы, и одна и та же формула применяется к движению планет. (Поскольку планеты и естественные спутники образуют пары сравнимой массы, расстояние r измеряется от общих центров масс каждой пары, а не от прямого общего расстояния между центрами планет.)

Если одна масса намного больше другой, удобно принять ее за эталон для наблюдений и определить ее как источник гравитационного поля, величина и ориентация которого задаются формулой:

граммзнак равно-граммMр2р^{\ displaystyle \ mathbf {g} = — {GM \ over r ^ {2}} \ mathbf {\ hat {r}}}

где — масса источника поля (большего размера), а — единичный вектор, направленный от источника поля к массе образца (меньшей). Отрицательный знак означает, что сила притягивает (указывает назад, к источнику).
M{\ displaystyle M}р^{\ displaystyle \ mathbf {\ hat {r}}}

Тогда вектор силы притяжения на массу образца можно выразить как:
F{\ displaystyle \ mathbf {F}}м{\ displaystyle m}

Fзнак равномграмм{\ Displaystyle \ mathbf {F} = м \ mathbf {g}}

Вот это трения , ускорение свободного падение поддерживается массами выборки под притяжением гравитационного источника. Это вектор, ориентированный к источнику поля, величина которого измеряется в единицах ускорения. Вектор ускорения свободного падения зависит только от того, насколько массивен источник поля и от расстояния r до массы образца . Это не зависит от величины малой массы образца.
грамм{\ displaystyle \ mathbf {g}}м{\ displaystyle m}M{\ displaystyle M}м{\ displaystyle m}

Эта модель представляет собой гравитационное ускорение «дальнего поля», связанное с массивным телом. Когда размеры тела нетривиальны по сравнению с интересующими расстояниями, принцип суперпозиции может быть использован для дифференциальных масс для предполагаемого распределения плотности по всему телу, чтобы получить более подробную модель гравитационного поля «ближнего поля». ускорение. Для спутников, находящихся на орбите, модели дальнего поля достаточно для грубых расчетов зависимости высоты от периода , но не для точной оценки будущего местоположения после нескольких орбит.

Более подробные модели включают (среди прочего) выпуклость на экваторе Земли и нерегулярные концентрации массы (из-за ударов метеоров) Луны. Миссия Gravity Recovery and Climate Experiment (GRACE), запущенная в 2002 году, состоит из двух зондов, получивших прозвище «Том» и «Джерри», которые находятся на полярной орбите вокруг Земли и измеряют разницу в расстояниях между двумя зондами, чтобы более точно определить гравитационное давление. поле вокруг Земли и отслеживать изменения, происходящие с течением времени. Точно так же миссия Лаборатории восстановления силы тяжести и внутренней обстановки в 2011-2012 годах состояла из двух зондов («Отлив» и «Поток») на полярной орбите вокруг Луны для более точного определения гравитационного поля для будущих навигационных целей и для получения информации о Внешний вид Луны.

Сила всемирного притяжения

С силой земного притяжения человечество знакомо с древности. Первые попытки объяснения этой силы предпринимались еще в античности. Птолемей, создавая свою систему мира, считал, что природа совершенна, и, поскольку самое совершенное место во Вселенной — это ее центр, то туда стремятся все тела. Именно поэтому Земля находится в центре Вселенной, именно поэтому орбиты Солнца и планет представляют собой хрустальные сферы, центр которых также совпадает с центром мира.

Рис. 1. Геоцентрическая система Птолемея с эпициклами.

С появлением гелиоцентрической системы мира, которая была значительно проще, чем геоцентрическая, объяснить падение тел «стремлением к центру» было уже нельзя. Стало ясно, что все тела притягиваются именно к Земле. Причина движения планет оставалась неизвестной.

Наиболее крупным шагом, приблизившим понимание гравитации, стало открытие законов Кеплера. Как раз к этому времени И. Ньютон пришел к выводу, что любое движение с ускорением — это результат действия силы. Поскольку движение по эллипсам — это движение с центростремительным ускорением, отсюда следовало, что между Солнцем и планетами существует сила, которая и приводит к изгибу траектории.

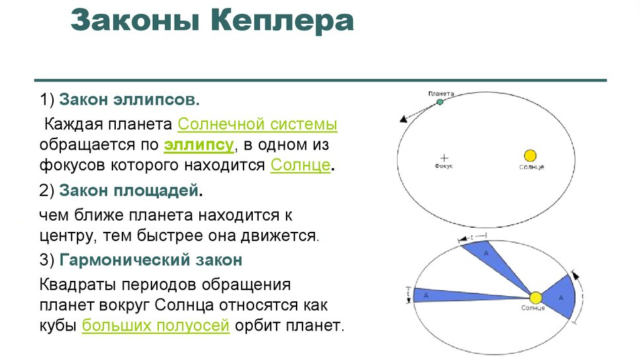Рис. 2. Законы Кеплера.

В результате на основе анализа законов Кеплера в 1667 г. И. Ньютон сформулировал закон тяготения

Еще более важно было распространение этого закона на все тела в природе вообще

В труде «Математические начала натуральной философии» была выведена формула силы гравитационного притяжения:

$$F=G{m_1m_2\over R^2}$$

Дальнейший успех применения этой формулы многократно подтверждал ее правильность, и дополнена она была лишь в начале XX в., с появлением релятивистской механики.

Закон всемирного тяготения

В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения F = G * (Mm/R2) F — сила тяготения M — масса первого тела (часто планеты) m — масса второго тела R — расстояние между телами G — гравитационная постоянная G = 6,67 × 10-11м3·кг-1·с-2

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей.

Задачка раз

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?

Решение

По закону всемирного тяготения сила притяжения планеты к звезде обратно пропорциональна квадрату радиуса орбиты. Таким образом, в силу равенства масс отношение сил притяжения к звезде первой и второй планет обратно пропорционально отношению квадратов радиусов орбит:

По условию, у первой планеты радиус орбиты вдвое больше, чем у второй, то есть R₁=2R₂.

Это значит, что:

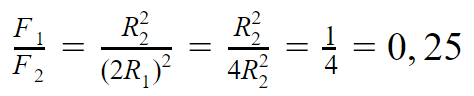
Ответ: отношение сил притяжения первой и второй планет к звезде равно 0,25.

Задачка два

У поверхности Луны на космонавта действует сила тяготения 144 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?

Решение

По закону всемирного тяготения сила притяжения космонавта со стороны Луны обратно пропорциональна квадрату расстояния между ним и центром Луны. У поверхности Луны это расстояние совпадает с радиусом спутника. На космическом корабле, по условию, оно в три раза больше. Таким образом, сила тяготения со стороны Луны, действующая на космонавта на космическом корабле, в 9 раз меньше, чем у поверхности Луны, то есть:

144 : 9 = 16 Н

Ответ: на расстоянии трех лунных радиусов от центра сила притяжения космонавта будет равна 16 Н.

Важный нюанс!

Правильно говорить не «на тело действует сила тяготения», а «Земля притягивает тело с силой тяготения».

Формула силы притяжения

Со времен Древней Греции философов интересовали явления притяжения тел к земле и свободного падения. К примеру, по утверждениям Аристотеля, из двух камней, брошенных с одинаковой высоты, быстрее достигнет земной поверхности тот, чья масса больше. В IV веке до нашей эры единственными методами научных изысканий служили наблюдения и анализ. К проверке гипотез опытным путем великие мыслители не прибегали. По истечению столетий физик из Италии Галилео Галилей проверил утверждения Аристотеля, используя практические методы исследований.

Итоги проведенных Галилеем опытов были опубликованы в «Беседах и математических доказательствах, касающихся двух новых наук». Ученый использовал псевдоним Сагредо: «пушечное ядро не опередит мушкетной пули при падении с высоты двухсот локтей». Формулировка закона всемирного тяготения была представлена в 1666 году Исааком Ньютоном. В ней фиксировались основные тезисы теоремы Галилея.

Смысл заключался в том, что тела, которые обладают разными массами, падают на землю с одинаковыми ускорениями.  Одно тело притягивает другое и, наоборот, с силой, которая прямо пропорциональна их массам и обратно пропорциональна отрезку пути между ними. Согласно определению гравитации от Ньютона, тела, характеризующиеся массой, обладают свойством, благодаря которому притягиваются друг к другу.

Понятие и определение

Силы взаимного притяжения – это силы, которые притягивают любые тела, обладающие массами.

Корректность выводов Ньютона неоднократно подтверждалась путем практических испытаний. Но в начале ХХ века перед учеными-физиками остро стоял вопрос о природе и характере взаимодействия крупных астрономических тел, включая разные виды планетарных систем и галактик в вакууме. Ньютоновского закона уже было недостаточно, чтобы решить эти задачи. Исключить недочеты позволила новая теория, разработанная Альбертом Эйнштейном в начале ХХ столетия. Общая теория относительности объясняет гравитацию не в качестве силы, а представляет ее в виде искривления пространства и времени в четырех измерениях, которое зависит от массы тел, создающих его.

Гравитация представляет собой свойство тел, которые характеризуются массой, притягивать друг друга. Данное физическое явление можно объяснить, как поле, оказывающее дистанционное воздействие на предметы, не связанные между собой никаким другим способом.

Достижение Эйнштейна не противоречит теоретическому объяснению гравитации от Ньютона. Общая теория относительности рассматривает закон всемирного тяготения, как частный случай, применимый для сравнительно небольших расстояний. Данная закономерность в настоящее время также активно используется для поиска решений задач на практике.